On teada, et pöördvõrdelise seose

graafikuks on hüperbool.

Hüperbooli üldine käsitlus on järgmine:

Hüperbooliks nimetatakse niisugust punktihulka tasandil, kus iga punkti kaugused (hüperbooli fokaalkaugused) kahest kindlast punktist (hüperbooli fookused) annavad jääva suurusega vahe.

 

Asümptoodiks nimetatakse sirgjoont, millele antud joon tõkestamatult läheneb.

Kui hüperbooli fookused on F₁(-c;0) ja F₂(c;0) ning fokaalkauguste vahe on 2a , siis on hüperbooli võrrandiks

Asümptootide võrrandid on

Analoogiliselt võib defineerida hüperbooli võrrandi kui fookused on y-teljel so F₁(0;-c) ja F₂(0;-c).

Hüperboolil, mille võrrand on

ning mille fookused on x-teljel, on x-teljega kaks lõikepunkti ( - a; 0) ja (  a; 0). Neid punkte nimetatakse hüperbooli haripunktideks.

Samuti saame öelda, et hüperboolil, mille võrrand on

ning mille fookused on y-teljel, on y-teljega kaks lõikepunkti ( 0; - a) ja ( 0; a). (Ka need on hüperbooli haripunktideks)

 

Hüperbooli haripunkte ühendavat lõiku, mille pikkus on 2a, nimetatakse hüperbooli reaalteljeks. Lõiku, mille pikkus on 2b, nimetatakse hüperbooli imaginaarteljeks.

Hüperbooli

imaginaartelg ühendab punkte ( 0; - b) ja ( 0; b).

Hüperbooli eksentrilisuseks nimetataksefookustevahelise kauguse ja reaaltelje suhet so

Hüperbooli puhul on alati c > a, seega  e > 1 . Hüperbooli eksentrilisus on alati ühest suurem.

 

Näiteks joonestame hüperbooli y²=4x²+16

Jagades võrrandi mõlemad pooled arvuga 16

saame

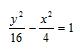
Seega saame, et graafik on sümmeetriline mõlema telje suhtes, graafik lõikub y-teljega punktides

(0; -4) ja ( 0; 4) - hüperbooli haripunktid

x - teljega graafik ei lõiku.

Asümptoodid on

Koostame tabeli hüperbooli sellele osale, mis jääb esimesse veerandisse

x	0	1	2	3
y	4	4,5	5,7	7,2

 

Selle hüperbooli fookused on punktides